Introduction & Purpose . This report was generated by the MatLab Report Generator Toolbox. It shows some simple MatLab commands and how easy it is to work with.
The Term Ergodic . The term ergodic is used in statistical physics, Markov chain theory and in time series analysis. In time series analysis, we say a covariance stationary time series is ergodic in the mean if the sample mean converges as the length of the time series increases to the mean over the distribution the ensemble or sample space of all possible time series. In Markov chain theory, a chain is said to be erodic if a limiting distribution exists for the states. In statistical physics, the ergodic hypothesis states for a gas in equilibrium, all states have an equal probability of realization. Our use of the term borrows from the usage in statistical physics. In simpler language, nonergodic really just means not equally probable.
Nonergodic property of Friday 13th . A surprising property of our calendar is that not all days of the week have equal chance of being the 13th of the month if you consider the long-run. For example, if you randomly select the 13th day of any month from all years between say 2,000 AD and 1,000,000,000,000 AD then the probability that it is Friday is exactly 43/300 which is slightly larger than 1/7. Moreover, in the long-run, the 13-th of the month has a higher probability of falling on a Friday than any other weekday.
Our Calendar Cycles . In the long-run, not every day of the week is equally probable of occurring on a given calendar date like the 13th of the month. The reason for this is due to the leap year effect which causes our calendar system to exactly cycle every 400 years and to the particular lengths chosen for our months. To show that the calendar cycles every 400 years, we compute the number of days in 400 years and note that it is divisible by 7.
365*400 + 100 -3
ans =
146097
mod(ans, 7)
ans =
0
Alternatively we can use the MatLab function weekday to verify this property.
WeekDays = str2mat('Sun', 'Mon', 'Tue', 'Wed', 'Thu', 'Fri', 'Sat');
WeekDays(weekday('1-Jan-2000'),:)
ans = Sat
WeekDays(weekday('1-Jan-2400'),:)
ans = Sat
We see that January 1, 2000 and January 1, 2400 both fall on a Saturday. Actually, there are shorter subcycles within the overall 400 year cycle. For example the next time the calendar for the year 2000 repeats is 28 years later. For 2001 though the calendar for 2007 is the same. The minimal complete cycle though has to take into account the leap centuries and so the minimal complete cycle turns out to be 400 years.
Now we evaluate the exact number of times each weekday falls on the 13th of the month for every month in the complete 400 year cycle. The array day13 contains a count for each day 1 thru 7, where we use the MatLab convention that Sunday is day 1, Monday is day 2, ..., Friday day 6 and Saturday day 7. The day number (1 to 7) for each 13th of the month is computed in the array year13.
months=str2mat('Jan','Feb','Mar','Apr','May','Jun','Jul','Aug','Sep','Oct','Nov','Dec');
day13=zeros(7,1); year13=zeros(400,7);total=0;
for i = 1:400;
for j = 1:12;
year = 2000+i-1;
jday = weekday(strcat(months(j,:),'-13-',num2str(year)));
day13(jday) = day13(jday)+1;
year13(i,jday) = year13(i,jday)+1;
total = total+1;
end
end
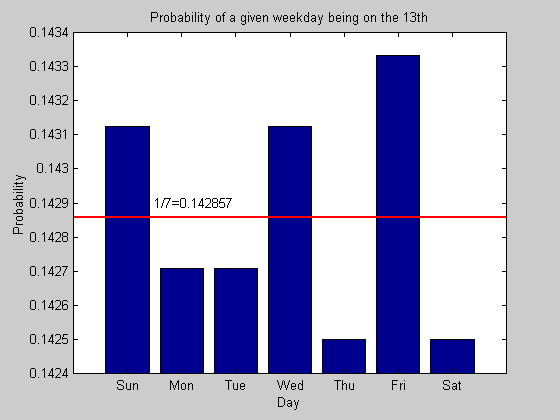
day13
day13 = 687 685 685 687 684 688 684
So we see there are a total of 688 Friday the 13ths and the next highest is 687 for Wednesday. The total number 13ths is 400*12 or 4800. So the exact probability of Friday the 13th is 688/4800=43/300. We compute the probabilities and plot them:
prob13 = day13/4800;
figure;
bar(prob13);
set(gca,'YLim',[0.1424 0.1434],'Layer','top');
set(gca,'XTickLabel',{'Sun';'Mon';'Tue';'Wed';'Thu';'Fri';'Sat'});
xlabel('Day');
ylabel('Probability');
title('Probability of a given weekday being on the 13th');
hold;
plot(0:8, repmat(1/7, 1, 9),'r', 'LineWidth', 2);
text(1.5,0.1429 ,'1/7=0.142857','Rotation',0,'FontSize',10);
hold;
Current plot held Current plot released

Next we investigate the distribution of weekdays which fall on the 13th on the month. At first glance it would seem that every year could have 13 possibilities for the number of Sunday the 13ths, ..., Friday the 13ths, etc. viz. (0, 1, ... , 12). So we count the number of times each weekday occurs on the 13th of the month in the array
dis13=zeros(7,13);
for i = 1:400;
for j = 1:7
nij = year13(i,j);
dis13(j,nij+1)=dis13(j,nij+1)+nij;
end
end
dis13
dis13 =
Columns 1 through 12
0 170 346 171 0 0 0 0 0 0 0 0
0 172 342 171 0 0 0 0 0 0 0 0
0 171 346 168 0 0 0 0 0 0 0 0
0 172 338 177 0 0 0 0 0 0 0 0
0 172 344 168 0 0 0 0 0 0 0 0
0 171 340 177 0 0 0 0 0 0 0 0
0 172 344 168 0 0 0 0 0 0 0 0
Column 13
0
0
0
0
0
0
0
So for any specific weekday the number of times it can be the 13th in a given year varies from 2 to 4 and for Friday we see that there are respectively 171, 340 and 177 times it occurs 1, 2 or 3 times in a year. Similarly, Saturday occurs 1, 2 or 3 times, 172, 344, 168 times every 400 years.
Next 28 Year Cycle . Over the next 28 year cycle, the 13-th is equi-probable for each weekday. From the next calculation, each weekday occurs 48 times as the 13-th of the month over this shorter cycle.
sum(year13(1:28,:))
ans =
48 48 48 48 48 48 48
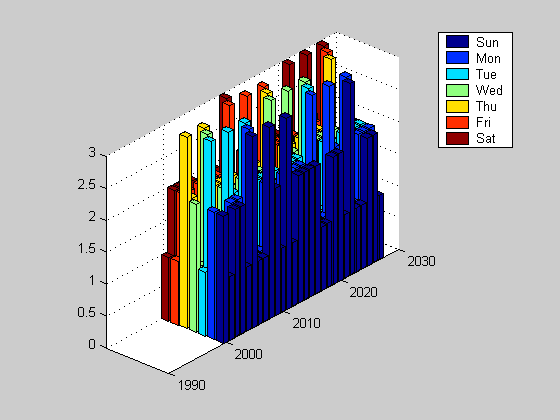
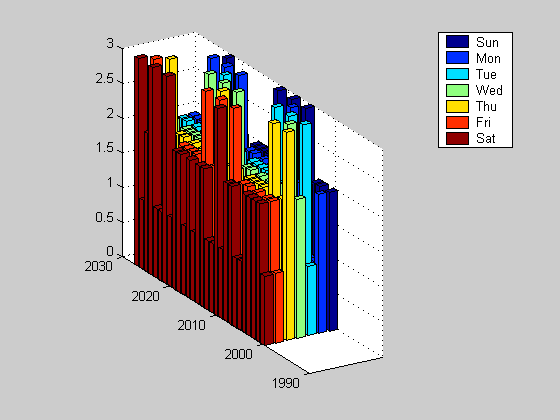
Distribution Over Next 28 Years . We can visualize the distribution of weekdays which occur on the 13th of the month using a 3D barchart. If you are using MatLab you can issue the command: rotate3d and this will enable you to rotate the 3D plot using your mouse. For this page, we just show the 3D plot from 2 different viewpoints.
bar3(2000:2027,year13(1:28,:)) view(-139, 28) legend(WeekDays)
bar3(2000:2027,year13(1:28,:)) view(149, 22) legend(WeekDays)
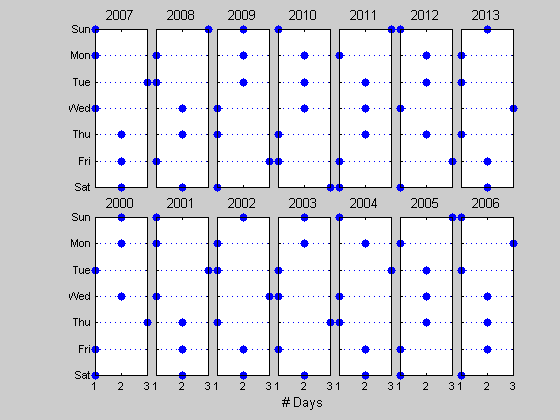
Multiway Dotplots . Although the 3D plot looks very nice, a more informative plot is the multiway dotplot. The multiway dotplot, developed in the 1980's by W.S. Cleveland, is often much better than such popular alternatives as bar charts and pie-charts. The dotchart is self-explanatory. More details on dotcharts are given in Cleveland's book Visualizing Data. Many of the graphical methods in Cleveland's book are available from a freely available toolbox: The Visualizing Data Toolbox. Here are dotcharts for the number of times each weekday occurs as the 13th of the month over the next 28 years.
years=num2cell(2000:2013); i=repmat(1:7, 2, 1); j=fliplr(repmat(1:2, 7, 1)); subloc=[reshape(j,14,1), reshape(i',14,1)]; figure; multidotplot(year13(1:14,:)', WeekDays, '# Days', years, subloc);
years=num2cell(2014:2028); figure; multidotplot(year13(1:14,:)', WeekDays, '# Days', years, subloc);
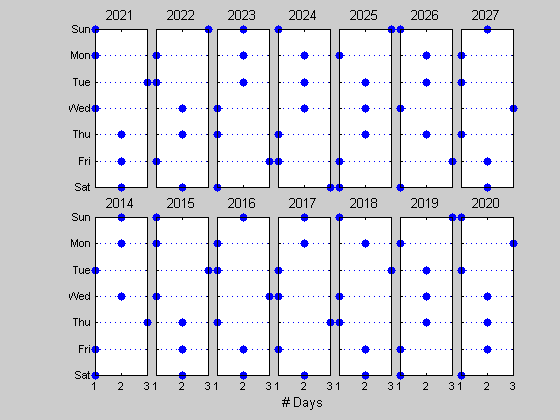
Conclusion . The statement that Friday the 13th is more probable than any other weekday is only true over the long-run when we consider at least 400 years or more. The MatLab commands used are available in the script file, friday.m