research - more project

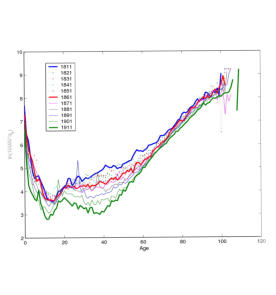
My Ongoing Projects: My current research is mainly carried out through the following ongoing research projects: • Phase-type Models of Mortality and Aging Process: It is of general interest to have a mortality law that can connect the observed age-specific mortality pattern with scientific (biological/generic/evolutionary) theory of aging and death. We believe that, only with a better understanding of the underlying processes involved, is it possible to incorporate the information such as medical developments and environmental or policy changes to make better mortality forecasts. My research in this area aims at providing a biological-based mortality law. In our preliminary study (see the paper "Markov Aging Process and Phase-type Law of Mortality", coauthored with X. Sheldon Lin, 2007), we have modeled a hypothetical aging process by a finite-state continuous-time Markov process with a single absorbing state. We have shown that the resulting phase-type mathematical representation is a flexible framework that can fit well the different shapes of mortality pattern appearing in historical data. Our recent paper, entitled "A subordinated markov model for stochastic mortality", has explored the use of matrix-analytic methodology in the valuation of mortality- linked derivatives. We have demonstrated mathematical tractability of Markovian mortality modeling framework in the field of actuarial and financial calculations. Our research in this area is highly innovative and promising. In the future research, we are interested in collaborating with people from medical science to work on Markovian model of aging index using empirical data as well. • Stochastic Mortality Modelling and Forecasting: There are so many factors that may affect future mortality changes. Consequently, there is always some degree of uncertainty in mortality prediction. I am interested in quantifying the degree of mortality uncertainty using stochastic models. In literature, many different models have been suggested to model mortality evolution, like the Lee-Carter or the Cairns-Blake- Dowd two factor models. I am also interested in developing statistical methods to properly assess the prediction performance of these models. The results of this research are important, for example, for management of public retirement system in dealing with mortality/longevity risk and for designing mortality risk transfer products using capital market. 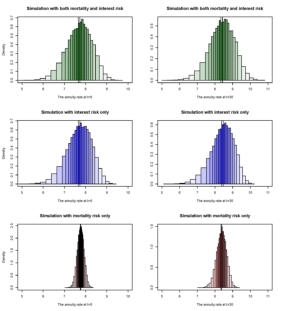• Evaluation of Insurance Policies under Mortality Risk and financial Risk: Recently, mortality risk has been recognized as systematic risk that can not be diversified by increasing the size of portfolio. This has completely altered the traditional actuarial perspective in which mortality risk can be treated as diversifiable. In the mean time, we see an increasing trend in the modern insurance market to embed different types of guaranteed features into insurance products --- the underlying risks involve both mortality risk and financial risks. All these indicate that modern insurance risk analysis has become more complex and requires innovative approaches to combine the expertise from both finance and actuarial science. My interest in this area is focused on developing analytical tools for the valuation, hedging and risk management of insurance products under the combined models.

Dept. of Statistical & Actuarial Sciences The University of Western Ontario 1151 Richmond Street, London Ontario, Canada N6A 5B7

Phone: 519-661-2111 ext 88233 Fax: 519-661-3813 Office: Western Science Centre 215 E-mail: xliu AT stats DOT uwo DOT ca

Associate Professor